4色定理
中々面白かったので紹介します。
四色定理とは
四色定理(よんしょくていり/ししょくていり、英: Four color theorem)とは、「平面上のいかなる地図も、隣接する領域が異なる色になるように塗り分けるには4色あれば十分だ」という定理です。
地図がどんなに複雑でも四色で塗れるというのが四色定理です。
主張が非常にシンプルで美しいため有名な定理です。
これを「地図の塗り分け」とすると、例えば飛び地を所属地と常に同じ色にしなければならない、とした場合、何色あっても足りない、といった問題などがあるので、「境界線によって囲まれたいくつかの領域からなる平面図形があり、境界線の一部を共有する(隣り合った)領域は異なった色で塗らなければならない、としたとき、4色あれば十分である」となります。
なお、境界線ではなく、点のみを共有する領域は隣り合っているものとはみなされず、互いに同色で塗ってもよいとします。
飛び地の場合と同じく、この条件なしではやはり何色あっても足りなくなります。
現実の地図では稀ですが、有名なものでは米国に、1点に4州が接する「フォー・コーナーズ」という地点があります。
3つの境界線が1点に集まっている場所があるため、3色必要であることはただちに明らかです。
続いて、ある領域の周囲にいくつかの領域がある場合(日本地図では長野県のような場合)を考えます。
周囲の領域の個数が偶数であれば3色で塗り分けできますが(長野県の場合はそうなる)、奇数個の領域で囲まれている場合は3色での塗り分けは不可能で、どうしても4色が必要です。
そして、4色あればどんな場合でも塗り分け可能なのか、ということが問題です。
このような領域の塗り分けが4色で可能となるのは平面(二次元)以下の次元までです。
三次元以上では領域の取り方次第でいくらでも色数が必要な例が作れます。
例えば「繋がったドーナツ」のような、穴がある形状の表面については7色必要です。
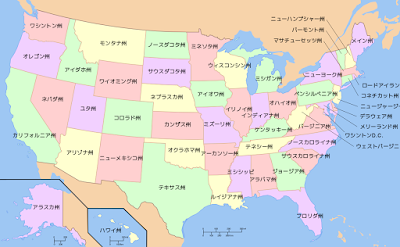
上図は(海や他国領土の色を除いて)4色に塗り分けられたアメリカ合衆国の州です。
歴史
1852年に法科学生のフランシス・ガスリー(Francis Guthrie)が数学専攻である弟のフレデリック・ガスリーに質問したのを発端に問題として定式化され、19世紀後半になって数学者がその話を聞いて証明を試みましたが、多くの数学者の挑戦をはねのけ続けてきました。
1879年、アルフレッド・ブレイ・ケンプ(Alfred Kempe)による証明が『アメリカ数学ジャーナル』誌上で発表されました。
この証明は妥当と見なされていましたが、1890年になってパーシー・ヒーウッド(Percy John Heawood)により不備が指摘されました。
しかし、ケンプの証明で使われた論理に沿って、地図を塗り分けるには5色で十分であることが証明されました。
これは五色定理と呼ばれています。
五色定理は、領域に分けられた平面、例えばある州を郡に分けた政治地図が与えられたとき、5種類以下の色を使って、隣接する領域が必ず別の色になっているように各領域を塗り分けられるという定理ですが、4色定理を弱くしたものです。
証明ははるかに易しく、1890年に パーシー・ジョン・ヒーウッドによって、五色定理は証明されました。
いま、地図上の領域の大きさや形は塗り分けの話には関係がなく、各領域が接している・接していないという情報だけが必要です。
各領域を頂点、接している領域同士を辺で結ぶ、という約束でどんな地図でも平面グラフに書き換えられます。
地図の塗りわけ問題は、平面グラフに置き換えることが出来ます。
地図の境界線をグラフの辺、境界線が接続する点をグラフの頂点としたグラフを作ると、グラフにおける頂点の彩色が、元の地図の塗分けと同じ問題となります。
グラフ理論により「平面グラフは4彩色可能である」という定理となります。
この4色で十分かどうかは、1852年以来長年、グラフ理論における最も有名な未解決問題として残りました。
1976年にケネス・アッペル (Kenneth Appel) とヴォルフガング・ハーケン (Wolfgang Haken) は、ヘーシュ(Heinrich Heesch)により考案された「放電」(discharging)と呼ばれる手続きを改良し、コンピュータを利用して約2000個の(後に1400個あまりに整理された)可約な配置からなる不可避集合を見出し、四色定理を「証明」するに至りました。
これは一応は認められましたが、人手による実行が(事実上)不可能なほどの複雑なプログラムの実行によるものであることから、ハードウェアやソフトウェア(コンピュータやそのプログラム)のバグの可能性などの懸念から、その確実さについて疑問視する向きもありました。
しかしその後、1996年にニール・ロバートソン (Neil Robertson) らによりアルゴリズムやプログラムの改良が行われ、より簡易な手法(従来の放電手続きよりシンプルな放電手続きを考案し、不可避集合の数を1405個から633個に抑えました)による再証明が行われるなど、第三者による複数の改良された証明が行われ、証明は確実視されるようになりました。
2004年にはジョルジュ・ゴンティエ (Georges Gonthier) が定理証明系Coqを用いて、よりシンプルな証明を行うなど、コンピュータの応用手法の洗練により、より確かな手続きで証明が行われるなどしているため、現在では四色問題は解決していると捉えられています。
証明
複雑に思える問題に対して簡潔にまとまった比較的短い証明(解答)を、エレガントな証明(解答)と言うことがあります。
証明
複雑に思える問題に対して簡潔にまとまった比較的短い証明(解答)を、エレガントな証明(解答)と言うことがあります。
四色定理のある種「コンピューターを使った力業な証明」は、これと対極にあるものとして揶揄を込めて「エレファント(象)」な証明とも言われます。
その後アルゴリズムは改良されましたが、現在でもコンピュータを使用しない証明は得られていません。
一般化
一般に種数 g ≥ 0 の閉曲面(わかりやすく言えば、穴が g 個あるドーナツ)を塗り分けるのに最低限必要な色の数は、1890年にヒーウッドによって
一般に種数 g ≥ 0 の閉曲面(わかりやすく言えば、穴が g 個あるドーナツ)を塗り分けるのに最低限必要な色の数は、1890年にヒーウッドによって
 ( ⌊ ⋅ ⌋ はフロア関数)
( ⌊ ⋅ ⌋ はフロア関数) と予想されました。
g ≥ 1 に対してこの予測が正しいことは、リンゲルとヤングスにより1968年に証明されました。
g = 0 を代入すれば、4 となります。
トーラス(円環、いわゆるドーナツの形)上のグラフは、7色で彩色可能です。