黄金比の不思議
「黄金比」とは言葉からしてミステリアスで、何か特別な響きがあります。
黄金比は、とても不思議な性質を持っており、身近な小さなものから、とてつもなく遠く巨大なものまで、実に様々なところで観られます。
黄金比とは
黄金比(おうごんひ、英語: golden ratio)は、
 の比です。
の比です。
 は、二次方程式 x2 − x − 1 = 0 の正の解であり、これを黄金数(おうごんすう、英語: golden number)といいます。
は、二次方程式 x2 − x − 1 = 0 の正の解であり、これを黄金数(おうごんすう、英語: golden number)といいます。
11,21,32,53,85,138,2113,3421,⋯
となり、これを計算して小数で表示すると、下記になります。
1, 2, 1.5, 1.66⋯, 1.6, 1.625, 1.6153⋯, 1.6190⋯, ⋯
 これを「1,1」の正方形まで続けていくと、下のような黄金長方形の黄金分割が出来上がります。
これを「1,1」の正方形まで続けていくと、下のような黄金長方形の黄金分割が出来上がります。 四角形の中に書いている数字は、その正方形の一辺の長さを示していますが、フィボナッチ数列になっています。
四角形の中に書いている数字は、その正方形の一辺の長さを示していますが、フィボナッチ数列になっています。
逆に長さ1の正方形を2つ並べて、隣の長辺側に長さ2の正方形を繋げ、次に長辺側に長さ3の正方形を繋げてを繰り返して、積んでいっても、同様に黄金長方形の黄金分割ができます。
黄金螺旋
黄金長方形の黄金分割で、赤い点で示した角の接点を、正方形の一辺の長さが半径になるような円弧で結んでいきます。 この赤い渦巻き状の螺旋がフィボナッチ数列から作られた「黄金螺旋」で、フィボナッチ螺旋とも呼ばれます。
この赤い渦巻き状の螺旋がフィボナッチ数列から作られた「黄金螺旋」で、フィボナッチ螺旋とも呼ばれます。
オウムガイの殻の模様は黄金螺旋を描いている、という説は有名です。
黄金比は、とても不思議な性質を持っており、身近な小さなものから、とてつもなく遠く巨大なものまで、実に様々なところで観られます。
黄金比とは
黄金比(おうごんひ、英語: golden ratio)は、
 の比です。
の比です。
近似値は1:1.618、約5:8もしくは8:13 です。
線分を a, b の長さで 2 つに分割するときに、a : b = b : (a + b) が成り立つように分割したときの比 a : b のことであり、最も美しい比とされます。
線分を a, b の長さで 2 つに分割するときに、a : b = b : (a + b) が成り立つように分割したときの比 a : b のことであり、最も美しい比とされます。
 は、二次方程式 x2 − x − 1 = 0 の正の解であり、これを黄金数(おうごんすう、英語: golden number)といいます。
は、二次方程式 x2 − x − 1 = 0 の正の解であり、これを黄金数(おうごんすう、英語: golden number)といいます。
しばしばギリシア文字の φ(ファイ)で表されますが、τ(タウ)を用いる場合もあります。
- 黄金数には,次のような性質があります。
二乗しても逆数をとっても、小数点以下は同じで、2乗はφに1を足し、逆数は1を引いた値となる不思議な性質を持っています。
作図
作図
最も簡単な作図方法は下記の通りです。
1.正方形 abcd を描きます。
2.辺 bc の中点 o を中心に、コンパスなどを用いて線分 oa または od を半径とした円を描きます。
3.2で描いた円と辺 bc の延長線との交点を e とし、長方形abefを描きます。
4.この時の長方形abefが、黄金比となります。
歴史
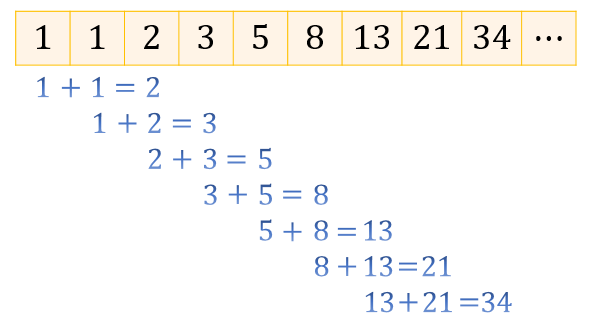
また隣り合う数で割ると次のようになります。
2.辺 bc の中点 o を中心に、コンパスなどを用いて線分 oa または od を半径とした円を描きます。
3.2で描いた円と辺 bc の延長線との交点を e とし、長方形abefを描きます。
4.この時の長方形abefが、黄金比となります。
歴史
伝承では、古代ギリシアの彫刻家ペイディアス (Φειδίας) が初めて使ったといわれます。
黄金数の記号φは彼の頭文字ですが、使われ始めたのは20世紀です。
レオナルド・ダ・ヴィンチも発見していた記録が残っています。
黄金数の記号φは彼の頭文字ですが、使われ始めたのは20世紀です。
レオナルド・ダ・ヴィンチも発見していた記録が残っています。
これを繰り返すと、黄金長方形は無限個の正方形で埋め尽くされます。
フィボナッチ数列
黄金長方形の黄金分割はフィボナッチ数列によって作ることができます。
フィボナッチ数列は、13世紀のイタリアの数学者フィボナッチが発表した数列です。
フィボナッチ数列
黄金長方形の黄金分割はフィボナッチ数列によって作ることができます。
フィボナッチ数列は、13世紀のイタリアの数学者フィボナッチが発表した数列です。
フィボナッチ数列(Fibonacci Sequence.)は「隣り合う2つの数を合計すると次の数になる数列」です。
書き並べていくと 1,1,2,3,5,8,13,21,34,55,⋯という数列になります。
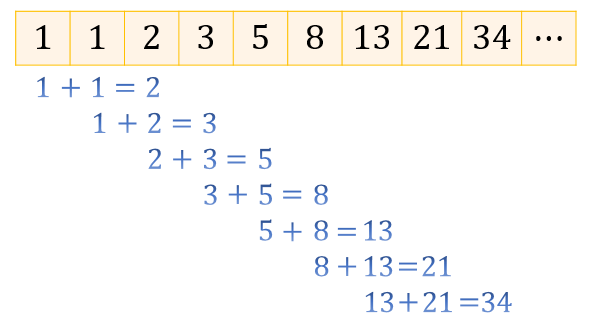
また隣り合う数で割ると次のようになります。
1, 2, 1.5, 1.66⋯, 1.6, 1.625, 1.6153⋯, 1.6190⋯, ⋯
限りなく先まで続けていくと、黄金比である1.618に近づいていきます。
次に黄金長方形の黄金分割を作ります。
フィボナッチ数列を「0,1,1,2,3,5,8,13,21,34,55,89 」まで用意し一番右の二つの数字、「55,89 」を使って長方形を作ります。
横の長さを89とし、縦の長さを55とします。 二つの数字を一つずらして、 「34,55 」の数で長方形を作ります。
二つの数字を一つずらして、 「34,55 」の数で長方形を作ります。
それを下の図ように上で作った長方形の右側に配置します。 次の「21,34」で作った長方形も同様に配置します。
次の「21,34」で作った長方形も同様に配置します。
次に黄金長方形の黄金分割を作ります。
フィボナッチ数列を「0,1,1,2,3,5,8,13,21,34,55,89 」まで用意し一番右の二つの数字、「55,89 」を使って長方形を作ります。
横の長さを89とし、縦の長さを55とします。
 二つの数字を一つずらして、 「34,55 」の数で長方形を作ります。
二つの数字を一つずらして、 「34,55 」の数で長方形を作ります。それを下の図ように上で作った長方形の右側に配置します。
 次の「21,34」で作った長方形も同様に配置します。
次の「21,34」で作った長方形も同様に配置します。
 これを「1,1」の正方形まで続けていくと、下のような黄金長方形の黄金分割が出来上がります。
これを「1,1」の正方形まで続けていくと、下のような黄金長方形の黄金分割が出来上がります。 四角形の中に書いている数字は、その正方形の一辺の長さを示していますが、フィボナッチ数列になっています。
四角形の中に書いている数字は、その正方形の一辺の長さを示していますが、フィボナッチ数列になっています。逆に長さ1の正方形を2つ並べて、隣の長辺側に長さ2の正方形を繋げ、次に長辺側に長さ3の正方形を繋げてを繰り返して、積んでいっても、同様に黄金長方形の黄金分割ができます。
黄金螺旋
黄金長方形の黄金分割で、赤い点で示した角の接点を、正方形の一辺の長さが半径になるような円弧で結んでいきます。
 この赤い渦巻き状の螺旋がフィボナッチ数列から作られた「黄金螺旋」で、フィボナッチ螺旋とも呼ばれます。
この赤い渦巻き状の螺旋がフィボナッチ数列から作られた「黄金螺旋」で、フィボナッチ螺旋とも呼ばれます。オウムガイの殻の模様は黄金螺旋を描いている、という説は有名です。
しかしその合理的な理由は知られておらず、実際にはオウムガイの殻のピッチは8度から10度であって、黄金螺旋のピッチ約17.03239度とはかけ離れているなどの、黄金螺旋ではないとの指摘もあります。
黄金螺旋に類似したものとしては、ひまわりの種、台風などの雲の渦、アンドロメダ星雲といった自然界の様々なところに存在しており、自然が作り出した造形美として知られています。
黄金比の応用
黄金比はパルテノン神殿やピラミッドといった歴史的建造物や美術品の中に見出すとされてきましたが、これらは後付けの都市伝説であるものが含まれています。
一方で、意図的に黄金比を意識して創作した芸術家も数多くいます。
長方形は縦と横との関係が黄金比になるとき、安定した美感を与えるという説があります。
これはグスタフ・フェヒナーの1867年の実験を論拠としています。
しかし、フェヒナーの実験の解釈については肯定的もしくは否定的な様々な見解があります。
「黄金比」は、建造物や美術品をはじめ、近代ではデザインや写真の構図などにも取り入れられています。
黄金長方形は、縦横のバランスが美しい、ということで、絵画の額などに使われています。
工学分野では、自動車ではスポーツカーやクロカン、セミトレーラー用トラクタや軽トラックのトレッド(輪距)とホイールベース(軸距)の関係が黄金比に近いです。
黄金比は、名刺を初め、様々なカード類の縦横比にも利用されることが多いです。
ディスプレイのアスペクト比には、WQXGA(解像度2560x1600)、WUXGA(同1920x1200)など、黄金比に近い8:5(16:10)のものもあります。
黄金螺旋に類似したものとしては、ひまわりの種、台風などの雲の渦、アンドロメダ星雲といった自然界の様々なところに存在しており、自然が作り出した造形美として知られています。
黄金比の応用
黄金比はパルテノン神殿やピラミッドといった歴史的建造物や美術品の中に見出すとされてきましたが、これらは後付けの都市伝説であるものが含まれています。
一方で、意図的に黄金比を意識して創作した芸術家も数多くいます。
長方形は縦と横との関係が黄金比になるとき、安定した美感を与えるという説があります。
これはグスタフ・フェヒナーの1867年の実験を論拠としています。
しかし、フェヒナーの実験の解釈については肯定的もしくは否定的な様々な見解があります。
「黄金比」は、建造物や美術品をはじめ、近代ではデザインや写真の構図などにも取り入れられています。
黄金長方形は、縦横のバランスが美しい、ということで、絵画の額などに使われています。
工学分野では、自動車ではスポーツカーやクロカン、セミトレーラー用トラクタや軽トラックのトレッド(輪距)とホイールベース(軸距)の関係が黄金比に近いです。
黄金比は、名刺を初め、様々なカード類の縦横比にも利用されることが多いです。
ディスプレイのアスペクト比には、WQXGA(解像度2560x1600)、WUXGA(同1920x1200)など、黄金比に近い8:5(16:10)のものもあります。



















